Difference between revisions of "Stormwater pollutant concentrations and event mean concentrations"
m |
m |
||
| Line 58: | Line 58: | ||
==Calculating emcs== | ==Calculating emcs== | ||
| − | |||
| − | |||
Emcs should represent the flow proportional concentration of a given pollutant parameter during storm events. The simplest way to calculate and emc is therefore to divide the total mass of a pollutant by the total runoff volume. Emcs can also be calculated as the sum, over multiple discrete time intervals within an event, of volume times the concentration for the time interval, divided by the total volume for the event | Emcs should represent the flow proportional concentration of a given pollutant parameter during storm events. The simplest way to calculate and emc is therefore to divide the total mass of a pollutant by the total runoff volume. Emcs can also be calculated as the sum, over multiple discrete time intervals within an event, of volume times the concentration for the time interval, divided by the total volume for the event | ||
| Line 67: | Line 65: | ||
[http://stormwaterbook.safl.umn.edu/pollutant-removal/analysis-individual-storm-events Erickson et al.] provide detailed discussion and examples for calculating pollutant loading from stormwater runoff. The emc calculated for a specific event is a function of the sampling method. Erickson et al. discuss the following methods for sampling. | [http://stormwaterbook.safl.umn.edu/pollutant-removal/analysis-individual-storm-events Erickson et al.] provide detailed discussion and examples for calculating pollutant loading from stormwater runoff. The emc calculated for a specific event is a function of the sampling method. Erickson et al. discuss the following methods for sampling. | ||
| + | |||
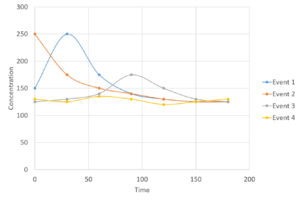
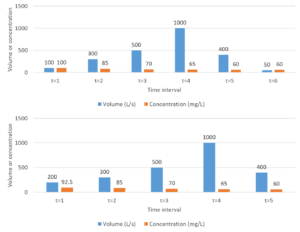
| + | [[File:EMC example 2.png|300px|thumb|alt=image for emcs|<font size=3>Example of how emcs can be calculated using concentration and flow data taken at discrete time intervals. In the top example, assume all time intervals are 30. In the lower graph, intervals 1 and 2 from the top graph are combined and Q and C average, while the remaining intervals are left at 30. The emc for the top graph is 69.1 mg/L and 76.0 mg/L for the lower graph, even though the data are the same.</font size>]] | ||
| + | |||
*Flow-weighted discrete samples: "When samples are collected based on a user-specified constant incremental volume of discharge (e.g., every 1000, 2000, or 5000 gallons) that passes the sampler, the samples are defined as flow-weighted. Each flow-weighted sample is assumed to represent the average pollutant concentration for the entire incremental volume of water to which it corresponds. Each discrete sample is stored in an individual container, and the contents of each container are analyzed separately." | *Flow-weighted discrete samples: "When samples are collected based on a user-specified constant incremental volume of discharge (e.g., every 1000, 2000, or 5000 gallons) that passes the sampler, the samples are defined as flow-weighted. Each flow-weighted sample is assumed to represent the average pollutant concentration for the entire incremental volume of water to which it corresponds. Each discrete sample is stored in an individual container, and the contents of each container are analyzed separately." | ||
*Flow-weighted composite samples: "Flow-weighted composite samples are collected every time a user-specified constant volume of flow passes the sampler and all samples are stored in a single container. To determine pollutant concentration, an aliquot is collected from the composite sample, and the concentration is assumed to represent that of the entire composite sample." | *Flow-weighted composite samples: "Flow-weighted composite samples are collected every time a user-specified constant volume of flow passes the sampler and all samples are stored in a single container. To determine pollutant concentration, an aliquot is collected from the composite sample, and the concentration is assumed to represent that of the entire composite sample." | ||
| Line 75: | Line 76: | ||
The sampling method affects the resulting calculation of emc. For example, in the adjacent image, emcs were calculated for the same runoff event. In the top portion of the image, sampling occurred every 30 minutes and the overall emc is 69.1 mg/L. In the lower portion of the image, the first two time intrvals were combined and Q and C averaged over the 60 minute time interval, while the remaining time intervals were 30 minutes each. The overall emc is 76.0 mg/L. The difference is a result of a bias toward higher concentrations in the early portion of the runoff event for the lower graph. This tendency toward higher pollutant concentrations in the early part of a runoff event is called the first flush. | The sampling method affects the resulting calculation of emc. For example, in the adjacent image, emcs were calculated for the same runoff event. In the top portion of the image, sampling occurred every 30 minutes and the overall emc is 69.1 mg/L. In the lower portion of the image, the first two time intrvals were combined and Q and C averaged over the 60 minute time interval, while the remaining time intervals were 30 minutes each. The overall emc is 76.0 mg/L. The difference is a result of a bias toward higher concentrations in the early portion of the runoff event for the lower graph. This tendency toward higher pollutant concentrations in the early part of a runoff event is called the first flush. | ||
| + | |||
| + | [https://fortress.wa.gov/ecy/publications/documents/1810026.pdf Washington State] developed standard operating procedures for measuring pollutant loads, including emcs. They include procedures for addressing seasonality. | ||
==Factors affecting emcs== | ==Factors affecting emcs== | ||
Revision as of 12:13, 9 April 2020
This page is in development
Because of the expense and difficulty of monitoring stormwater runoff, we often rely on published information to estimate pollutant loading associated with runoff. Models or other tools are often used to predict pollutant loading. These models and tools require information on the pollutant concentration in runoff. For example, the Simple Method, which is commonly used to estimate pollutant loading, utilizes the following equation
\(L = 0.227 P P_j R_v C A\)
where
- L = Load of a pollutant in pounds per year;
- P = Rainfall depth per year (inches);
- Pj = Fraction of rainfall events that produce runoff;
- Rv = Runoff coefficient, which expresses the fraction of rainfall which is converted into runoff. Rv = 0.05 + 0.009(I);
- I = Site imperviousness (i.e., I = 75 if site is 75% impervious);
- C = Flow-weighted mean concentration of the pollutant in urban runoff (mg/l); and
- A = Area of the development site (acres).
This page provides a discussion of pollutant concentrations in stormwater runoff, including a review of literature and recommended values to use
Contents
- 1 Factors affecting actual and measured storm concentrations
- 2 Event mean concentrations
- 3 Calculating emcs
- 4 Factors affecting emcs
- 5 Literature review of event mean concentration (emc) values)
- 6 Recommended event mean concentration (emc) values
- 7 Data on event mean concentrations
- 8 References
- 9 Related pages
Factors affecting actual and measured storm concentrations
The actual concentration of a pollutant in stormwater runoff varies with several factors, including but not limited to
- land use,
- time between runoff events,
- duration and intensity of runoff,
- characteristics of the pollutant,
- season, and
- connectedness of impervious surfaces.
In addition, the measured concentration varies with these factors and factors related to measurement, including but not limited to
- type of sampling equipment and sample collection,
- location of sampling,
- frequency of sampling,
- laboratory analysis, and
- data analysis.
This variability presents challenges in estimating pollutant loading, but having accurate estimates of pollutant concentrations is necessary to accurately calculate pollutant loading and reductions in loading associated with implementation of stormwater practices and to accurately select and design appropriate practices to treat runoff.
Event mean concentrations
In the absence of monitoring data for a specific study or location, we often use event mean concentrations (emc). The emc represents the average pollutant concentration for a given stormwater event, expressed in units of mass per volume (e.g., mg/L). Given the number of factors affecting pollutant concentration, determining an appropriate emc is challenging.
Despite challenges in accurately determining emcs, they are widely used in stormwater applications. Emcs are used in many stormwater water quality models and calculations of pollutant loading. They are therefore fundamental to understanding pollutant loads and how to address reducing pollutant loads in stormwater runoff.
Calculating emcs
Emcs should represent the flow proportional concentration of a given pollutant parameter during storm events. The simplest way to calculate and emc is therefore to divide the total mass of a pollutant by the total runoff volume. Emcs can also be calculated as the sum, over multiple discrete time intervals within an event, of volume times the concentration for the time interval, divided by the total volume for the event
\( emc = (∫^t_0 C_tQ_td_t) / (∫^t_0 Q_td_t) ≅ (Σ C_tQ_tΔt) / (ΣQ_tΔt) \)
where Ct and Qt are the concentration and flow volume over a discrete time interval dt (Δt).
Erickson et al. provide detailed discussion and examples for calculating pollutant loading from stormwater runoff. The emc calculated for a specific event is a function of the sampling method. Erickson et al. discuss the following methods for sampling.
- Flow-weighted discrete samples: "When samples are collected based on a user-specified constant incremental volume of discharge (e.g., every 1000, 2000, or 5000 gallons) that passes the sampler, the samples are defined as flow-weighted. Each flow-weighted sample is assumed to represent the average pollutant concentration for the entire incremental volume of water to which it corresponds. Each discrete sample is stored in an individual container, and the contents of each container are analyzed separately."
- Flow-weighted composite samples: "Flow-weighted composite samples are collected every time a user-specified constant volume of flow passes the sampler and all samples are stored in a single container. To determine pollutant concentration, an aliquot is collected from the composite sample, and the concentration is assumed to represent that of the entire composite sample."
- Time-weighted discrete samples: "Time-weighted discrete samples are collected at a user-specified, constant time interval (e.g., 30 minutes), and each sample is stored in a separate container and analyzed separately. Because the magnitude of the discharge during a natural storm event varies over time, each time-weighted sample does not represent a constant volume of discharge."
- Time-weighted composite samples: "Time-weighted composite samples are collected at equal time increments, and all samples are stored in a single container. ... Time-weighted composite sampling is not recommended."
- Discrete grab samples: "A grab sample is a single sample collected at one location over a relatively short time period, typically sampling the entire cross-section of water. Discharge must be accurately and continuously measured and the time of each grab sample must be recorded to assess pollutant removal performance. Discrete samples are stored in individual containers, and the contents of each container are analyzed separately."
- Composite grab samples: "Composite grab samples are typically collected at variable time and volume increments and stored in a single sample storage container. Composite grab sampling is not recommended."
The sampling method affects the resulting calculation of emc. For example, in the adjacent image, emcs were calculated for the same runoff event. In the top portion of the image, sampling occurred every 30 minutes and the overall emc is 69.1 mg/L. In the lower portion of the image, the first two time intrvals were combined and Q and C averaged over the 60 minute time interval, while the remaining time intervals were 30 minutes each. The overall emc is 76.0 mg/L. The difference is a result of a bias toward higher concentrations in the early portion of the runoff event for the lower graph. This tendency toward higher pollutant concentrations in the early part of a runoff event is called the first flush.
Washington State developed standard operating procedures for measuring pollutant loads, including emcs. They include procedures for addressing seasonality.
Factors affecting emcs
Many factors affect the emc. The most important factors and how to address them are dicussed below.
| First flush is a phenomenon in which pollutant concentrations in stormwater runoff are greater in the early portion of a runoff event. First flush is common for relatively uniform land use settings, for winter and early spring runoff events, and for runoff events during fall leaf-drop. During dry periods between runoff events, pollutants build-up on impermeable surfaces. For Type 2 rain events, initial rain intensity is low and increases through a storm before decreasing near the end of the storm. The initial runoff is therefore highly concentrated with pollutants that have accumulated on impermeable surfaces. As runoff volume increases during an event and pollutants become more resistant to being washed off, concentrations decrease and typically reach steady state. First flush is not universally applicable to stormwater runoff, however. For example, if higher pollutant buildup on impermeable surfaces occurs in upper portions of a watershed, as might occur in an area with variable land uses, the peak concentration may be delayed as those higher pollutant loads take time to reach a receiving point. Similarly, some pollutants may be resistant to transport in early stages of an event. In other situations, concentrations in runoff may be uniform throughout an event, particularly if rainfall intensities are uniform and pollutants are soluble (e.g. chloride). |
Land use
Because of the variability in emcs across different land uses, it is beneficial to consider different land uses when calculating pollutant loads. Compositing emcs across land uses is generally not recommended.
Some generalizations about pollutant loading as a function of land use include the following.
- Commercial, industrial, and transportation land use typically have higher percentages of impervious and directly connected impervious surface, as shown in the accompanying table summarizing curve numbers for different land uses. This results in more efficient delivery of pollutants and runoff compared to other land uses. Consequently, we expect higher emcs from these land uses for smaller runoff events and when pollutant buildup on impermeable surfaces is greater, and lower emcs for larger runoff events with greater rainfall intensities as a result of dilution.
- Nutrient (phosphorus, nitrogen) concentrations are greater in residential areas and other land uses that contribute significant amounts of organic material to impermeable surfaces. Dissolved fractions also comprise a greater percent of the total load for these pollutants when the source of the nutrient is organic material.
- Concentrations of metals increase as road density and traffic volume increase.
- Concentrations of petroleum-related compounds and polycyclic aromatic hydrocarbons (PAHs) increase as road density and traffic volume increase.
- Concentrations of total suspended solids (TSS) may be similar across different land uses, but the characteristics of the TSS varies. Organic fractions make up a larger percent of TSS in residential areas and other land uses where there are sources of organic material to impermeable surfaces, while inorganic fractions (e.g. sand, silt) comprise the majority of TSS in settings with low inputs of organic material.
- Bacteria concentrations are typically greater in residential areas due to greater inputs from domestic animals (e.g. dogs), birds, and other animals. Studies also suggest irrigated lawns and leaves/organic material on impermeable surfaces contribute to bacteria loads.
- In cold climates where deicers are applied, chloride concentrations are a function of deicer application rates. Chloride concentrations are therefore highly variable in areas where deicers are applied. Also note that within a land use receiving high inputs of chloride-deicers, chloride emcs vary with season.
- Oxygen demand is typically related to the amount of organic carbon in runoff. Thus, land uses with greater inputs of organic material (e.g. residential) will have greater oxygen demand.
- Concentrations of several organic chemicals, such as pesticides and chlorinated compounds, varies. Factors affecting concentrations include industrial sources, presence of contaminated sites, historic use of these materials, and atmospheric deposition.
- Although the potential for nutrient and bacteria loads is greater in lower density residential areas, the lower amount of directly connected impervious surface typically results in lower emcs for lower density residential land use.
- Pollutant concentrations in open, forested, and park areas are lower, primarily due to reduced impervious surface.
- There is limited information on many of the newer chemicals, such as commercial-consumer compounds, veterinary and human pharmaceuticals, lifestyle and personal care compounds, and others. These chemicals, generically labeled as contaminants of emerging concern (CEC), have variable sources, including industry, sediment, and atmospheric deposition. For more information, see Fairbairn et al. (2018), Maruya (2013), Masoner et al. (2019), and Kiesling et al. (2019).
Curve numbers for antecedent moisture condition II (Source USDA-NRCS).
Link to this table
| A | B | C | D | |
|---|---|---|---|---|
| Meadow - good condition | 30 | 58 | 72 | 78 |
| Forest | ||||
| Poor | 45 | 66 | 77 | 83 |
| Fair | 36 | 60 | 73 | 79 |
| Good | 30 | 55 | 70 | 77 |
| Open space | ||||
| Poor | 68 | 79 | 86 | 89 |
| Fair | 49 | 69 | 79 | 84 |
| Good | 39 | 61 | 74 | 80 |
| Commercial 85% impervious | 89 | 92 | 94 | 95 |
| Industrial 72% impervious | 81 | 88 | 91 | 93 |
| Residential | ||||
| 1/8 acre lots (65% impervious) | 77 | 85 | 90 | 92 |
| 1/4 acre lots (38% impervious) | 61 | 75 | 83 | 87 |
| 1/2 acre lots (25% impervious) | 54 | 70 | 80 | 85 |
| 1 acre lots (20% impervious) | 51 | 68 | 79 | 84 |
| Impervious areas | 98 | 98 | 98 | 98 |
| Roads (including right of way) | ||||
| Paved | 83 | 89 | 92 | 93 |
| Gravel | 76 | 85 | 89 | 91 |
| Dirt | 72 | 82 | 87 | 89 |
| Row crops | ||||
| Straight row - good | 67 | 78 | 85 | 89 |
| Contoured row - good | 65 | 75 | 82 | 86 |
| Pasture - good | 39 | 61 | 74 | 80 |
| Open water | 99 | 99 | 99 | 99 |
Effects of season
- Ranges of EMCs are largest in spring
- Median EMCs for chloride, total phosphorus (TP) and total nitrogen (TN) are greater in winter
- Median concentrations of many chemicals is higher in the initial spring flush
- Summer has the potential to increase the bacteria EMC and illustrate the seasonal differences.
Effects of time between rain events
Effects of connectednedd of impervious surface
Literature review of event mean concentration (emc) values)
Recommended event mean concentration (emc) values
As a result of our literature review we developed recommended emc values. These are summarized in the following table.
For phosphorus and total suspended solids, we developed a broader discussion of emcs. We suggest you read these sections if using emcs for your stormwater applications.
Phosphorus emcs
Data from the following studies was used to generate emcs for total phosphorus.
- National Stormwater Quality Database. This dataset provides data from several nationwide studies. We used only data from region 1, which includes Minnesota and states with similar rainfall patterns. Data were compiled for four land uses: Commercial (n=165), industrial (n=84), residential, (n=249), and open space (n=6).
- Lin (Review of Published Export Coefficient and Event Mean Concentration (EMCs) Data. This report includes summaries of multiple studies conducted in North America. Data existed for all land uses included in the table presenting recommended emcs.
- Washington District Department of the Environment - Selection of Event Mean Concentrations (EMCs). This study summarized data from studies in the Washington D.C. area. Land uses included commercial, roadway/highway, industrial, forest/open, and residential.
- U.S. Environmental Protection Agency, 1983, Results of the Nationwide Urban Runoff Program—Executive summary. Land uses included commercial and residential.
- Urban Stormwater Quality, Event-Mean Concentrations, and Estimates of Stormwater Pollutant Loads, Dallas-Fort Worth Area, Texas, 1992–93. Included commercial (n=42), residential (n=77), industrial (n=63) land uses.
- A review of sediment and nutrient concentration data from Australia for use in catchment water quality models . A compilation of multiple studies from Australia. Included forest (n=68) and mixed (n=36) land uses.
- Characterization of Urban Runoff Pollution between Dissolved and Particulate Phases . Study of five sites in China. Land uses included roof and transportation (roads).
- Quality Of Wisconsin Stormwater, 1989-94. Samples from mixed land use in Wisconsin (n=204).
- Analysis of Nonpoint Source Pollution Runoff from Urban Land Uses in South Korea. 23 samples in Korea from high density residential, medium desntiy residential, industrial, institutional land uses.
- Seasonal Performance Variations for Storm-Water Management Systems in Cold Climate Conditions. 15 samples from transportation land use in New Hampshire.
- Determination of event mean concentrations and first flush criteria in urban runoff. 31 samples from transportation land use in Los Angeles.
- Multiple linear regression models of urban runoff pollutant load and event mean concentration considering rainfall variables. 45 samples from commercial, industrial, and high density land uses.
- Stormwater runoff driven phosphorus transport in an urban residential catchment: Implications for protecting water quality in urban watersheds. 29 events from low density land use in Florida.
- Sources of phosphorus and street dirt from Two Urban Residential Basins in Madison, Wisconsin, 1994-95. 25 samples from medium density land use in Wisconsin.
- Nutrient Sources in Urban Areas – A Literature Review. Report summarizing multiple studies in Colorado. Land uses include residential, mixed, commercial, and open space.
- Contribution of surface runoff from forested areas to the chemistry of a through-flow lake. Forested land use in Poland.
The following table summarizes results from our literature review. The table includes a range of values observed in the literature. Note this range does not represent a statistically-derived range but instead is based on a combination of data analysis and best professional judgement. For example, we did analyze the data for outliers, but also omitted entire studies if we felt the data were not representative of typical conditions likely to be encountered in Minnesota. To see the full range of values compiled from the literature, open the Excel spreadsheet containing the data.
Event mean concentrations for total phosphorus.
Link to this table
| Land cover/land use | Range (mg/L) | Recommended value (mg/L) | Notes |
|---|---|---|---|
| Commercial | 0.20 - 0.34 | 0.200 | If applicable to models being used, adjust curve numbers/runoff coefficients when calculating loads |
| Industrial | 0.23 - 0.55 | 0.235 |
|
| Residential | 0.26 - 0.38 | 0.325 | Concentrations vary widely depending on local conditions |
| High-density/Multi-family residential | 0.28 - 0.40 | Calculate1 |
|
| Medium density residential | 0.18 - 0.40 | Calculate1 |
|
| Low density residential | 0.24 - 0.40 | Calculate1 |
|
| Freeways/transportation | 0.25 - 0.45 | 0.280 |
|
| Mixed | 0.16 - 0.84 | 0.290 |
|
| Parks and recreation | Use value for open space or calculate |
|
|
| Open space | 0.12 - 0.31 | 0.190 | |
| Conventional roof | 0.01 - 0.20 | 0.030 | |
| Institutional | 0.14 - 0.422 | See note |
|
| Forest/shrub/grassland | 0.03 - 0.45 | 0.090 | Concentrations are likely to vary with season in areas with fall leaf drop |
| Open water and wetlands | see Notes (next column) |
|
|
| Cropland (row crops) | 0.126-1.348 | 2 | Median from our review = 0.533 |
| Pasture | 0.35-0.45 | 2 |
1The link takes you to information on calculating event mean concentrations for areas with multiple land uses.
2Our literature review was not extensive enough to warrant a specific recommend emc for this land use
Dissolved and particulate phosphorus
In many places in this manual and in the MIDS calculator, we assume that particulate phosphorus accounts for 55 percent of total phosphorus and dissolved phosphorus for 45 percent of total phosphorus.
Data on event mean concentrations
Below are data we've compiled during our literature review.
- National Stormwater Quality Database. The National Stormwater Quality Database (NSQD) is an urban stormwater runoff characterization database developed under the direction of Dr. Robert Pitt, P.E., of the University of Alabama and the Center for Watershed Protection under support from the U.S. Environmental Protection Agency.
References
- Brezonik PL, Stadelmann TH.. 2002. Analysis and predictive models of stormwater runoff volumes, loads, and pollutant concentrations from watersheds in the Twin Cities metropolitan area, Minnesota, USA. Water Res. Apr;36(7):1743-57. DOI: 10.1016/s0043-1354(01)00375-x
- Maniquiz, Marla C. , Soyoung Lee, Lee-Hyung Kim. 2010. Multiple linear regression models of urban runoff pollutant load and event mean concentration considering rainfall variables. Jour Environ. Sci. 22:6:946-852.
- Maniquiz, Marla C., Jiyeon Choi, Soyoung Lee, Hye Jin Cho, Lee-Hyung Kim. 2010. Appropriate Methods in Determining the Event Mean Concentration and Pollutant Removal Efficiency of a Best Management Practice. 15:215-223.
- Pan X, Jones KD. 2012. Seasonal variation of fecal indicator bacteria in storm events within the US stormwater database. Water Sci Technol. 65(6):1076-80. doi: 10.2166/wst.2012.946.
- Schiff, Kenneth C., and Liesl L. Tiefenthaler. 2011. Seasonal flushing of pollutant concentrations and loads in urban stormwater. Jour. Amer. Water Works Assoc. 47:1:136-143.
- Tiefenthaler, L.L., K. C. Schiff, and M. K. Leecaster. 1997. Temporal variability patterns of stormwater concentrations in urban stormwater runoff.
https://fortress.wa.gov/ecy/publications/documents/1810026.pdf