Estimating the water balance for a stormwater and rainwater harvest and use/reuse site
A water balance must be calculated to determine if the desired capture volumes can be achieved and to properly size the system. A water balance consists of estimating the amount of water that can be captured and the amount of water that is used. Key considerations include balancing the amount of storage unit overflow with the size of the storage unit, and limiting or eliminating the need for a secondary water supply.
For stormwater management, it is recommended to evaluate source areas (harvest and use supply) first and then identify candidate use applications. Calculations of water captured are a function of rainfall and runoff potential from the site. For system design, we recommend using a calculator that uses a daily time step and summarizes the volume in the storage unit on a daily basis. The Minnehaha Creek Watershed District calculator can be used for these calculations. This calculator was developed and funded by the Mississippi Watershed Management Organization and Minnehaha Creek Watershed District. The calculator utilizes an Excel spreadsheet that allows the user to enter information on irrigation use, catchment (watershed) area, and storage. Inputs can be manipulated to determine catchment size, amount used, or needed storage. Guidance on using this calculator, along with example calculations and other methodologies for completing water balance, are found here.
A summary of available stormwater harvest and use calculators and models can be found in the section on calculating credits for stormwater and rainwater harvest and use. Either one model can be chosen that estimates all components of the water budget, or a mix of models can be used. For example, the output from calculators that estimate indoor and outdoor use on a daily basis (e.g., SFPUC Non-Potable Water Demand Calculator) can be combined with daily watershed runoff volumes and pollutant loads predicted from an existing watershed model (e.g., SWMM) for a site to estimate the performance of a stormwater harvest and use system.
A model for stormwater harvest and use design should include the following:
- Uses daily precipitation
- Accounts for variable evapotranspiration rates
- Generates water budget components (overflow, inflow, indoor uses, outdoor uses) time series on a daily basis
- Accounts for supplemental water supply
For simple irrigation use systems, we recommend using the Minnehaha Creek Watershed District calculator. This calculator was developed and funded by the Mississippi Watershed Management Organization and Minnehaha Creek Watershed District. The calculator utilizes an Excel spreadsheet that allows the user to enter information on irrigation use, catchment (watershed) area, and storage. Inputs can be manipulated to determine catchment size, amount used, or needed storage. Guidance on using this calculator, along with example calculations and other methodologies for completing a water balance, are found here.
The Met Council Water Balance Tool and the VDCR Cistern Design Spreadsheet are other useful calculators for calculating a water balance where supplemental water use is needed for year-round indoor water uses. The Met Council calculator provides output that must be copied into a spreadsheet or other tool, where sizing calculations can be made. The Virginia calculator utilizes Virginia rainfall data, which limits its applicability in Minnesota, but the calculator incorporates a wide range of indoor use applications.
Some calculators, such as North Carolina’s calculator, utilize mean monthly rainfall. While monthly Minnesota rainfall data is easy to obtain and using monthly data provides an easy method of calculation, this approach can introduce significant errors since rainfall is not uniform throughout a month. Because stormwater harvest and use systems are designed to store a certain size rainfall event for use prior to the next rainfall event, the timing and intensity of rainfall on a daily basis is just as important to the monthly rainfall total. For example, less runoff volume reduction is possible if two large rainfall events occur back to back compared to if they occur further apart.
Information on calculating water balance is also provided in the 2011 Met Council Reuse Guide (see Quantity and Storage Worksheet, A.2w for a list of steps to balance the volume of water that can be captured and stored (supply) with the volume of water to be used (demand)).
If no models are available, water and phosphorus budgets for a stormwater harvest and use system can be calculated by hand in a spreadsheet. See the Calculating the Water Budget and Calculating the Phosphorus Budget sections below.
Contents
Calculating the water budget
The water budget should be estimated using a daily time step, mass balance approach. Daily changes in basin volume (VB) are equal to watershed runoff (QW) inputs less evaporation (QE), overflow (QO), and indoor/outdoor use (QU) outputs.
To determine the water balance for a site, the following components are needed:
- Estimate of the watershed runoff generated from the drainage area on a daily basis
- Daily mass-balance of the storage system, either a cistern or pond
- Estimate of daily use for indoor or outdoor uses on a daily basis
- Watershed Runoff
If no models are available, watershed runoff volume and pollutant loads can be estimated by hand using a daily rainfall record, land cover curve numbers, and event mean concentrations (i.e., the Simple Method).
Stormwater harvest and use is highly dependent on the timing and intensity of rainfall. Using at least 5 to 10 years of continuous daily rainfall is preferred for modeling the expected performance across a broad range of rainfall timing and intensities. That is to say, for the same total annual precipitation, rainfall can be distributed in smaller but more frequent events, or in larger but less frequent events. Daily rainfall can be downloaded from the Minnesota State Climatology Office. Gridded precipitation data] can be used to generate continuous rainfall records in areas without a long-term gage nearby. This tool also provides monthly and year-to-year summary statistics to aid the selection of a representative range of rainfall data to design the stormwater harvest and use system.
Curve numbers and event mean concentrations can be selected using guidance found here.
- Basin Volume
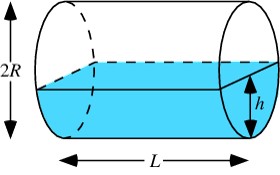
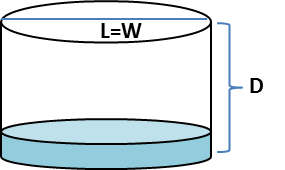
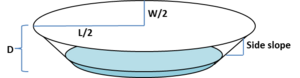
For either a cistern or a pond, a depth-area or depth-volume curve needs to be generated based on the design parameters. For ponds, a continuous depth-volume curve can be generated by interpolating based on depth, area and volume information at each available bathymetric contour. Or the pond can be simplified as an ellipsoid with constant side slope as shown below. Cisterns can be modeled as a simple vertical or horizontal cylinder. Equations for determining the volume (V) of water in a vertical and horizontal cylinder are shown below.
\( V_{horizontal cylinder} = L (R^2 cos^{(-1)} ((R - h)/R) - (r - h)sqrt(2Rh - h^2)) \)
\( V_{vertical cylinder} = π(W/2)^2 (D - h) \)
\( V_{stormwaterpond} = Σ_{z=0}^h πz(L - 2s(D - h))(W - 2s(D - h)) \)
where:
- L = horizontal length
- W = horizontal width
- D = height of basin
- R = radius
- h = depth or height of water in a basin
- s = side slope
The key difference between ponds and cisterns in a water budget calculation is evaporation. Evaporation losses from the surface of a storage pond can be a significant loss of water in an annual budget. Evaporation from the surface of an enclosed cistern would be negligible compared to evaporation from the surface of a pond exposed to wind and direct sunlight. Pond surface evaporation is also dependent on the surface area of the pond, which changes with changing depth based on the pond side slope.
Evaporation is calculated based on a variable pond surface area with changing water depth assuming a constant side slope of the basin. As a result, evaporation from ponds designed with a safety bench may be underestimated in the model if only the side slope of the storage pool is used as an input to the model. For more accurate model results, an average side slope of the storage pool and the safety bench should be used. Refer to the U of M Stormwater Book for information on calculating evaporation.
It is also important to determine the initial basin volume. Constraints should ensure the basin volume at least as great as the sediment storage volume but no greater than the total volume of the basin. An initial basin volume needs to be chosen based on the expected operation of the system, i.e., empty if storage is a cistern and is emptied prior to winter, or full if storage is a pond that ices over in winter.
Water demand
Several tools are available for determining indoor and outdoor water demand (see table below). The San Francisco Public Utilities Commission (SFPUC) Non-Potable Water Calculator provides the most input options for determining indoor and outdoor water demand. Note that these calculators may be subject to change or revision following publication of this wiki.
Irrigation rates are an important consideration for determining irrigation water demands. Irrigation rates can be higher for more well-drained soils (e.g., sand) compared to more poorly-drained soils. However, stormwater harvesting and irrigation use is usually used in lieu of infiltration BMPs in poorly-drained soils to reduce stormwater volumes through plant evapotranspiration. Therefore, irrigation rates should not exceed plant potential evapotranspiration (PET) rates in poorly-drained soils. If local PET rates are unknown, the SFPUC Non-Potable Water Calculator can be modified with local soil and plant characteristics for determining appropriate irrigation rates.
| Water demand calculators | ||
|---|---|---|
| Sponsoring agency/organization | Calculator name, version, and date | Calculator download and documentation |
| Virginia Department of Conservation and Recreation (VDCR) | Cistern Design Spreadsheet Version 1.6, March 2010 | [1] |
| San Francisco Public Utilities Commission (SFPUC) | Rainwater Harvesting Calculator 2016 | [2] |
| San Francisco Public Utilities Commission (SFPUC) | Non-Potable Water Calculator | [3] |
Water budget equations
A water budget can be estimated without a model using the following equations in a spreadsheet. To determine watershed Flow, QW, use the following equations.
\( S_{pervious or impervious} = (1000 / CN_{pervious or impervious}) - 10 \)
If rainfall depth, R (inches), is less than 0.2 * S, then runoff = 0. If rainfall depth (inches) is greater than or equal to 0.2 * S, then runoff (inches) is given by
\( Runoff_{pervious or impervious} = (R - 0.2 * S)^2 / (R + 0.8 * S) \)
Watershed flow, Q (cubic feet), is given by
\( Q_{pervious} = ((1 - I/100) A_W Runoff_{pervious} / 12) \)
\( Q_{pervious} = ((1 - I/100) A_W Runoff_{impervious} / 12) \)
\( Q_{watershed} = Q_{pervious} + Q_{pervious} \)
where
- I = percent imperviousness;
- AW = watershed area;
- Qpervious = flow generated from pervious fraction of the drainage area; and
- Qimpervious = flow generated from impervious fraction of the drainage area.
The basin surface area (AB) is given by
\( A_B = πL/W (((V_B - V_{B, max} + π/72 L^2 W) * (W^2/L^2 9/π))^{1/3})^2 \)
where
- L = length of basin and
- W = width of basin.
The basin volume (VB in cubic feet) is given by
\( V_B = V_{B-1} + Q_W - Q_E - Q_O - Q_U \)
where
- VB-1 is the basin volume on the previous day;
- QE is the evaporation volume;
- QO is the overflow volume; and
- QU is the indoor/outdoor use.
\( Q_E = E/12 A_B \)
\( Q_O = V_{B-1} + Q_W - Q_E - V_{B,max} \)
\( Q_U = V_{B-1} + Q_W - Q_E - Q_O \)
- or
\( Q_U = demand/7.48/7 \)
- whichever is less
where
- E is evaporation in inches;
- VB,max is the maximum volume of the basin before overflow occurs;
- demand is the rate of total outdoor and indoor non-potable demand in gallons per week; and
- 7.48 and 7 are conversion factors.
Calculating the phosphorus budget
A major water quality benefit of stormwater harvest and use is the potential phosphorus reduction benefits, both through sedimentation processes and by irrigation uses. A phosphorus budget can be estimated to account for these benefits. The phosphorus budget should account for the total load entering the basin, any mixing and sedimentation occurring in the basin, and any outputs from the basin, such as overflow and distribution to indoor or outdoor uses.
Sedimentation can be calculated by hand using empirical equations published in William W. Walker Jr. (1987) PHOSPHORUS REMOVAL BY URBAN RUNOFF DETENTION BASINS, Lake and Reservoir Management, 3:1, 314-326, DOI: 10.1080/07438148709354787.
When watershed runoff enters a pond or cistern (basin), phosphorus attached to larger particles (usually sediment) falls out (sedimentation) of the water and settles on the storage basin floor. The longer watershed runoff remains in a basin (i.e., longer residence times) the more phosphorus sedimentation occurs, although most phosphorus sedimentation occurs within the first several days. Therefore, it can be assumed that if water flowed into the basin on a day without overflow, the maximum amount of phosphorus retention occurred. If water flowed into the basin on a day with overflow, the maximum phosphorus sedimentation should be decreased in relation to the decreasing residence time (calculated from the overflow rate and maximum basin depth). Note that there are three main fractions of phosphorus (P): water column dissolved P, water column particulate P, and sediment bound particulate P. Sedimentation involves only the transfer of water column particulate P to sediment bound particulate P. Therefore, phosphorus removal by sedimentation depends on the fraction of total phosphorus that is particulate phosphorus.
A daily phosphorus mass balance can be estimated for a stormwater pond in a spreadsheet using the following steps. First, the watershed phosphorus load and watershed volume enter the basin and, on that same day, completely mix with the basin phosphorus load and basin volume from the previous day to determine an intermediate phosphorus concentration in the basin with no change in volume (i.e., no overflow). For this step only, the calculated basin volume may exceed the actual basin volume. Next, sedimentation, overflow and irrigation are assumed to occur with a corresponding volume and phosphorus load based on the intermediate pond phosphorus concentration. Finally, a new basin concentration is calculated based on the remaining phosphorus load in the basin and the new basin volume calculated for that day from the water mass balance described above.
A phosphorus budget can be estimated without a model using the following series of empirical equations published in William W. Walker Jr. (1987) PHOSPHORUS REMOVAL BY URBAN RUNOFF DETENTION BASINS, Lake and Reservoir Management, 3:1, 314-326, DOI: 10.1080/07438148709354787.
Residence time (T, years) is given by
\( T = V_B/Q_O/365 \)
where
- VB is the volume of the basin (ft3)
- QO = overflow volume (ft3); and
- 365 is a conversion factor.
Surface overflow (QS) is given by
\( Q_S = 0.3048D_B / T \)
where DB is the maximum basin depth.
The second order decay rate (K2) is given by
\( K_2 = (0.056 Q_S/F_O) / (Q_S + 13.3) \)
where FO is the phosphorus concentration of watershed runoff (mg/L) divided by the orthophosphorus concentration of watershed runoff (mg/L)
The reaction rate (NR) is given by
\( N_R = K_2 T C_{W - TP} \)
The retention coefficient (Cp) is given by
\( R_P = 1 - (1 - (1 + (4N_R))^{0.5})/2N_R \)
The pond phosphorus concentration (CP), in milligrams per liter (mg/L), is given by
\( C_P = ((C_{P-int} (V_{B-1} + Q_W)) - P_O - P_I)/V_B \)
where
\( C_{P-int} = ((C_{P-1} V_{B-1} + ((1 - R_P) Q_W C_{W-TP}))/1000) / (V_{B-1} + Q_W) \)
where
- CP-1 is the phosphorus concentration in the pond on the previous day;
- VB-1 is the basin volume on the previous day; and
- QW is the watershed runoff volume.
Watershed total phosphorus load (PW-TP), in pounds per day, is given by
\( P_{W-TP} = 0.0000624Q_B C_{W-TP} \)
where
- the first term is for unit conversion;
- QB is in cubic feet per day; and
- CW-TP is in mg/L.
Phosphorus load to overflow (PO), in pounds per day, is given by
\( P_O = 0.0000624Q_O C_{P-int} \)
where
- the first term in the above equation is for unit conversion;
- QO is in cubic feet per day; and
- CP-int is in mg/L.
Phosphorus load to indoor/outdoor uses (PU), in pounds per day, is given by
\( P_U = 0.0000624Q_U C_{P-int} \)
where
- the first term in the above equation is for unit conversion;
- QU is in cubic feet per day; and
- CP-int is in mg/L.
Phosphorus load to sediment (PS), in pounds per day, is given by
\( P_S = P_{W-TP} R_P \).
Phosphorus load in the pond (PP), in pounds, is given by
\( P_P = 0.0000624C_P V_B \)
where
- the first term in the above equation is for unit conversion;
- QO is in cubic feet per day; and
- CP-int is in mg/L.
This page was last edited on 17 January 2023, at 14:25.